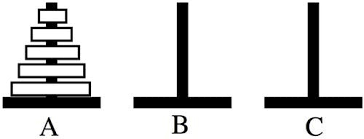
### Towers of Hanoi ###  Above are the 'Towers of Hanoi,' a classical mathematical puzzle dating back to 1883. Disks are aligned such that the largest disc is at the bottom and each disc above is smaller. You may slide these disks to other towers under a constraint and mission - Constraint: During any move, you may not place a larger disc on top of a smaller one. - Goal: Move all disks to tower $C$ in the minimal amount of moves One question we could ask about this game is what is the minimum number of moves needed to solve the puzzle? To answer this, we can proceed as follows: 1. Notate: Define $T_n$ to be the minimum number of moves it takes to move $n$ discs from peg $A$ to peg $B$. We see $T_0 = 0$, $T_1 = 1$, and $T_2 = 3$. 2. Find an upper bound (a sufficient method defined recursively): To solve the puzzle for $n$ discs, it suffices to move $n-1$ pegs to tower $B$, move the largest disc to tower $C$, and move the $n-1$ pegs from $B$ to $C$. Thus, $T_n \leq 2T_{n-1}+1$. 3. Argue that the upper bound is the lower bound (argue the sufficient method is necessary): For the largest peg to move from the bottom of tower $A$ to the bottom of tower $C$, there must be no discs above it on $A$ (otherwise we cannot move it) and there cannot be any discs on tower $C$ since otherwise we would break the rules by placing a larger disc on top of a smaller one. This means that the $n-1$ smaller discs must all be on tower $B$ in order. We do not know how many times the largest disc was moved prior to this realization so we critically must perform at least $2T_{n-1}+1$ moves to solve the puzzle meaning $T_n \ge 2T_{n-1}+1$ so $T_n = 2T_{n-1}+1$ for $n>0$ and for $n=0,$ $T_0 = 0$. 4. Find a closed form. We may guess a reasonable formula that holds for small cases satisfying our newfound recurrence relation or we may proceed with deliberation. One nice idea is to notice that $T_0+1=1,\quad T_n+1 = 2T_{n-1}+2.$ From here, define $U_n := T_n+1$. Then, $U_{n+1} = 2U_n$ for $n >0$ meaning $U_{n} = 2^n$ and so $T_n=2^n-1$. This process is nice to generalize ### Lines in the plane ### Let $L_n$ denote the maximum number of divided regions of the plane given there are $n$ lines drawn. How would be solve for $L_n$? As we will see, simple observations cascade to an interesting, non-trivial solution. Note that if we draw a new line, then $k$ regions are added if and only if the new line passes through $k$ regions. Further, a line passes through $k$ regions if and only if it intersects $k-1$ other lines. So, given $n-1$ lines in the plane, drawing a new line that is pairwise non-parallel to the others means the new line passes through the $n-1$ other lines, creating $n$ new regions. So $L_0 = 1$ and $L_n = L_{n-1}+n$ for $n\ge 1$. I claim by induction that for $n \ge 1$, $L_n = \frac{n(n+1)}{2}+1$. The base case is true, so assume that $L_n = \frac{n(n+1)}{2}+1$ and notice that $L_n+(n+1) = \frac{n(n+1)}{2}+1+(n+1) = \frac{(n+1)(n+2)}{2}+1$ as desired.